Step 1: Write out the formula for the distance between two points on the Cartesian plane
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)

Step 2: Use the formula to find the distance KM between points K and M.
In this case,
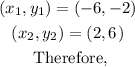
![\begin{gathered} d=\sqrt[]{(2-(-6))^2+(6-(-2))^2}=\sqrt[]{(2+6)^2+(6+2)^2} \\ d=\sqrt[]{8^2+8^2}=\sqrt[]{64+64}=\sqrt[]{128}\approx11.3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/730ypp058vi0faxkf7xjylr7l51ih2sshh.png)
Hence, KM = 11.3 units
Step 3: Use the formula to find the distance KL between points K and L.
In this case,
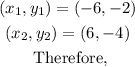
![\begin{gathered} d=\sqrt[]{(6-(-6))^2+(-4-(-2))^2}=\sqrt[]{(6+6)^2+(-4+2)^2} \\ d=\sqrt[]{12^2+(-2)^2}=\sqrt[]{144+4}=\sqrt[]{148}\approx12.2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tr12xftf6rfb0m8mb8k6tv9gw1yjt6nkpp.png)
Hence, KL = 12.2 units
Step 4: Use the formula to find the distance LM between points L and M.
In this case,
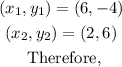
![\begin{gathered} d=\sqrt[]{(2-6)^2+(6-(-4))^2}=\sqrt[]{(-4)^2+(6+4)^2} \\ d=\sqrt[]{16^{}+(10)^2}=\sqrt[]{16+100}=\sqrt[]{116}\approx10.8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d7rh5lz8lieexnenelyabvmhqg4xdwgz60.png)
Hence, LM = 18.9 units
Step 4: Find the perimeter of the triangle KLM
The perimeter of the triangle is given by the sum of the sides of the triangle.
That is,
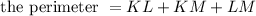
Therefore,
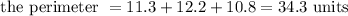
Hence, the perimeter of triangle KLM is 34.3 units