Question

Hello please help me understand this. this is a review for a test tomorrow.

Answer 1

We have the original line, which is represented as

`4y=3x+7`

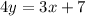
Just to make things easier, let's write the same equation another way

`4y-3x=7`

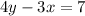
That's the same equation! just rewrote.

We can easily find the transformed line using the fact that the image is always parallel to the ore-image (original equation), then, we must find the parallel equation!

We have

`4y-3x=7`

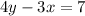
And we will look, which one is parallel to it? Simple! any equation that has

`4y-3x\text{ or }3x-4y`

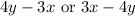
On the left side, the number on the right side (without "x" and "y") doesn't matter.

Looking at our options, we can see that we have the following equation:

`3x-4y`

Then we can affirm that

`3x-4y=9`

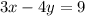
Is parallel, see that if we multiply all by (-1) we get

`\begin{gathered} 3x-4y=9 \\ 4y-3x=-9 \end{gathered}`

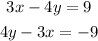
The left side here is the same, then it's parallel, if it's parallel, it could represent its image.

____________________________ Second explanation

Let's use the slope-intercept form for the original equation, we have

`4y=3x+7`

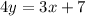
If we divide both by 4 we get

`y=(3)/(4)x+(7)/(4)`

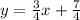
See that

`m=(3)/(4)`

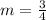
Then we will look for a linear equation that has the same slope! if it has the same slope, it means they're parallel, then let's transform each equation in slope-intercept form.

To the right to the left we have

`3x+4y=9\Rightarrow y=-(3)/(4)x+(9)/(4)`

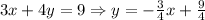
The slope here is m = -3/4, not 3/4, then it's not parallel.

`4x+3y=9\Rightarrow y=-(4)/(3)x+(9)/(4)`

Again, m is not 3/4, not parallel.

`3x-4y=9\Rightarrow y=(3)/(4)x-(9)/(4)`

Here the slope is 3/4, it's parallel to the original equation, then it's the correct answer 3x - 4y = 9.

And the last one

`4x-3y=9\Rightarrow y=(4)/(3)x-(9)/(4)`

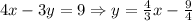
The slope here is 4/3, wrong too