Given the three end points (3,8), (5,20/3) and (6,5) which are written in the form of (x1,y1), (x2,y2) and (x3,y3).
Write out the formula to obtain the equation of the parabola
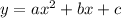
Write out the given coordinates
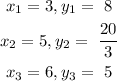
Substitute the coordinates into the given equation above to obtain the three equations
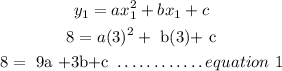
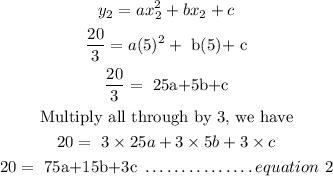
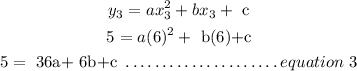
Combining the three equations together
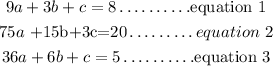
Hence, the three equations above are the equations of the parabola with three unknowns a,b and c.