Step 1: Write out the expression
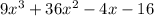
Step 2: Group the expressions and factorize
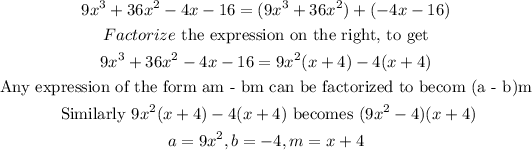
Step 3: Factorize 9x² -4 using the "AC" method
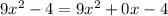
To use the "AC" method we find the product of the constant -4 and the coefficient of x²,9. The product is -36.
Next, we find two real numbers such that their product is -36 and their sum is the coefficient of x, which in this case is 0.
Consider the real numbers +6 and -6.
Their product is given by
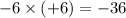
Their sum is given by
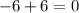
Hence, we have found our two numbers.
Therefore,
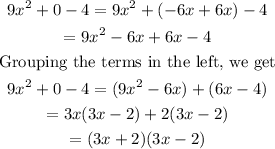
Therefore,
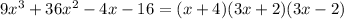
Hence the polynomial 9x³ + 36x² -4x -16 is factored completely to
(x + 4)(3x + 2)(3x - 2)