By the definition of definite integral, the integral of a function in a interval is the sum of the areas above the x-axis subtracted by the areas below the x-axis inside of the interval.
Given the function
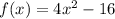
Since our function is an upward parabola and our interval is [-2, 2], and those are the roots of our function, the whole region is under the x-axis, therefore, the area we want is minus the integral of our function on this interval.

Since we're dealing with an integral of a pair function in a symmetric interval, we can rewrite our integral as
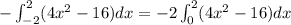
Multiplying an integral by (-1) is the same as inverting the order of the limits.
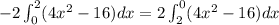
To find the area, we can just solve the integral

And this is our answer.