Question

For questions 3 - 4, determine the 8th term in the following sequences. 3) 1, 2, 4, 8, ... 4) a= 216, r=-6

Answer 1

In this sequence, we can see that a_1 =1. a_2 =2. NOte that

`(a_2)/(a_1)=2`

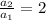
Also, note that

`(a_3)/(a_2)=(4)/(2)=2`

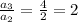
If we do this term by term, we can see that if we take one term and divide it by the previous one, we will always get the number 2.

This type of sequence receives the name of a geometric sequence, where

`a_n=a\cdot r^(n-1)`

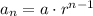
where a is the first term, r is the common ratio (the one obtained from dividing one term by the previous one)