EXPLANATION
Given:
GF = 15 CG = 23
By the Quadrilateral theorem
GF = GD = 15 and CG = GE = 23
We can now apply the relationship given for the kite geometry as follows:
CD^2 = GD^2 + CG^2
As GD = GD, replacing terms:

Solving the powers:
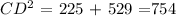
Applying the square root to both sides:
![CD=\sqrt[]{754}=27.45\text{ square units}](https://img.qammunity.org/2023/formulas/mathematics/college/2msj4sriqbwud6mx9b0qm46b8hsfkc44vg.png)
The value of CDIS 27.45 square units