Question

2. Janelle deposits $2,000 in the bank. The bank will pay 5% interest per year,compounded annually. This means that Janelle's money will grow by5% each vear.a. Make a table showing Janelle's balance at the end of each year for 5 years.b. Write an equation for calculating the balance b at the end of any year t.c. Approximately how many years will it take for the original deposit todouble in value? Explain your reasoning.d. Suppose the interest rate is 10%. Approximately how many years will ittake for the original deposit to double in value? How does this interest ratecompare with an interest rate of 5%?

Answer 1

a)

Since the bank pays 5% each year, then the balance after one year will be 105% of the original balance.

To find the balance after one year, calculate what is 105% of 2000 equal to by multiplying 2000 times 105/100:

`2000*(105)/(100)=2000*1.05=2100`

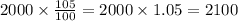
The same process is repeated the next year, where the balance will be equal to 105% of 2100:

`2100*(105)/(100)=2100*1.05=2205`

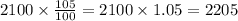
And so on. To find the balance on the third year, multiply 2205 by 1.05:

`2205*1.05=2315.25`

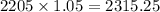
The balance on the fourth year will be:

`2315.25*1.05=2431.0125`

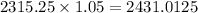
And in the fifth year:

`2431.0125*1.05=2552.563125`

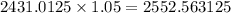
Therefore, the table will include the following data:

`\begin{matrix}\text{Year} & \text{Balance} \\ 1 & 2100 \\ 2 & 2205 \\ 3 & 2315.25 \\ 4 & 2431.0125 \\ 5 & 2252.563125 \\ \end{matrix}`

B)

Since each year the balance gets multiplied by 1.05, then after t years the balance would increase by a factor of 1.05^t.

Since at year 0 the balance was $2000, then the equation that models the balance b after t years is:

`b=2000*1.05^t`

C)

To find how many years it will take for the original deposit to double in value, set b=4000 and solve for t:

`\begin{gathered} 4000=2000*1.05^t \\ \Rightarrow(4000)/(2000)=1.05^t \\ \Rightarrow2=1.05^t \\ \Rightarrow t=\log _(1.05)(2) \\ \therefore t=14.2\approx14 \end{gathered}`

It will take approximately 14 years for the balance to double.

D)

If the interest rate was 10%, then each year the balance would increase by a factor of 110/100, which is equal to 1.1.

Then, the model for the balance as a function of time would be:

`b=2000*1.1^t`

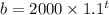
And the time that it would take for the balance to double would be:

`t=\log _(1.1)(2)=7.27\approx7`

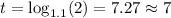
Then, it would take approximately 7 years for the balance to double if the interest rate was 10% instead of 5%.