For this problem, we are given a certain function:
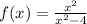
We need to determine the critical values, the intervals where the function is increasing or decreasing, and the relative extremum.
The critical numbers are the points at which the derivative is equal to 0:
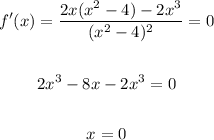
Therefore the critical values are:

The function is increasing whenever its derivative is positive, and it is decreasing when the derivative is negative. The derivative is shown below:
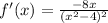
The denominator is always positive since it is powered by 2, therefore the numerator will determine the signal of the expression. Whenever the value of x is negative, the whole expression will be positive, with this we can conclude that the function is increasing for negative x, and decreasing for positive x. We need to consider that the function is not defined for x = -2 or 2, therefore the intervals need to exclude these values.
The intervals are:
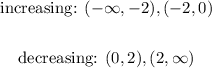
In the first step, we calculated the point at which the derivative is equal to zero, these are critical points and they represent a value of maximum or minimum. In order to determine which type of critical point it is, we need to calculate the second derivative, if the second derivative has a positive value, then it is a minimum. This is shown below:
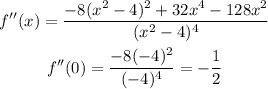
With this, we can say that the point (0,0) is a local maximum and that the function does not have a local minimum.