We are asked to determine the wavelength of a 0.14 kg object with a speed of 1x10^-3 m/s. To do that we will use the following formula:
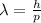
Where:

The momentum "p" is given by:
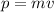
Where:
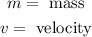
Substituting the momentum in the formula for the wavelength:
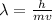
Plank's constant is equivalent to:
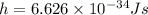
Substituting the values we get:
![\lambda=\frac{6.626*10^(-34)Js}{(0.14\operatorname{kg})(1*10^(-3)(m)/(s))}]()
Solving the operations:
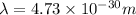
To compare this wavelength with the wavelength of a high-speed electron moving 1/10 of the speed of light we will determine the quotient between the two wavelengths:
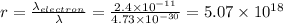
Therefore, the wavelength of the electron is 5.07x10^18 times larger than the wavelength of the ball.