Question

A boy sits at the top of a 3.00 mlong playground slide, tilted at 41.0°,with hk0.230. How fast is hegoing at the bottom?(Hint: Leave mass as a symbol,and it will cancel out.)(Unit = m/s)

Answer 1

Given data

The sliding distance is s = 3 m

The angle of inclination is 41 degree

The friction coefficient is 0.23

The free-body diagram of the above configuratin is shown below:

The expression for the force in the direction of motion is given as:

`\begin{gathered} ma=mg\sin \theta-f_k \\ ma=mg\sin \theta-\mu_{k_{}}mg\cos \theta \\ a=g\sin \theta-\mu_{k_{}}g\cos \theta \\ a=9.8m/s^{2^{}}*\sin 41\circ-0.23*9.8m/s^{2^{}}*\cos 41\circ \\ a=4.73m/s^2 \end{gathered}`

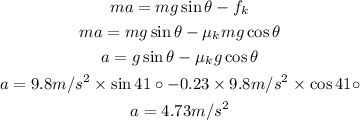
The expression for the velocity at the bottom is given as:

`\begin{gathered} v^2=2as \\ v=\sqrt[]{2as} \\ v=\sqrt[]{2*4.73m/s^{2^{}}*3\text{ m}} \\ v=5.327\text{ m/s} \end{gathered}`

Thus, the velocity of the boy at the bottom is 5.327 m/s.