1 Answer

Mitchell V · Answer 1 · 2023-07-04T06:12:58+0000

We are given the point (-3,2). We want the equation of the line that passes through this point and that is perpendicular to the line 2x-4y=10.

First, to solve this problem, we will write the given line equation in the slope -intercept form That is:

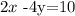
$2x\text{ -4y=10}$

we subtract 10 on both sides to get

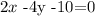
$2x\text{ -4y -10=0}$

now, we add 4y on both sides to get

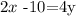
$2x\text{ -10=4y}$

Finally we divide both sides by 4, so we get

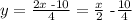
$y=\frac{2x\text{ -10}}{4}=(x)/(2)\text{ -}(10)/(4)$

from this equation, we can see that the slope of the given line is 1/2.

Now, to calculate the line we will use the following fact. The product of the slopes of two perpendicullar lines is -1.

Let m be the slope of the line we are looking for. Due to this fact we have the equation

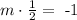
$m\cdot(1)/(2)=\text{ -1}$

so if we multiply both sides by 2, we get that

$m=\text{ -2}$

so now we know that the slope of the line should be -2.

So we know that the slope is -2 and that is passes through the point (-3,2). Then, we use this formula

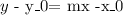
$y\text{ - y\_0= m\lparen x -x\_0\rparen}$

where (x0,y0) is the point through which the liness passes. That is, in our case (-3,2). So we get

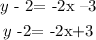
$\begin{gathered} y\text{ - 2= -2\lparen x -\lparen-3\rparen\rparen} \\ y\text{ -2= -2\lparen x+3\rparen} \end{gathered}$

now we add 2 on both sides, so we get

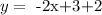
$y=\text{ -2\lparen x+3\rparen+2}$

if we distribute the product, we get

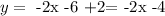
$y=\text{ -2x -6 +2= -2x -4}$

so the equation of the line is y=-2x-4

Please log in or register to add a comment.