Write the partial fraction decomposition (x )/((6x - 5)(5x + 1))

Question

Write the partial fraction decomposition
`(x )/((6x - 5)(5x + 1))`

Answer 1

Since the degree of the denominator is 2 and the degree of the numerator is 1, the form of the partial decomposition is given as

`(x)/((6x-5)(5x+1))=(A)/(6x-5)+(B)/(5x+1)`

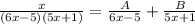
By rewriting the right hand side as a single fraction, we have

`(x)/((6x-5)(5x+1))=(A(5x+1)+B(6x-5))/((6x-5)(5x+1))`

We can to note that the denominators are equal, so we requiere the equality of the numerator, that is

`x=A(5x+1)+B(6x-5)`

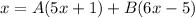
Then, by distributing A and B into their respective parentheses, we get

`x=A5x+A+B6x-5B`

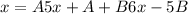
Now, by factoring x, we obtain

`x=x(5A+6B)+A-5B`

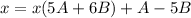
The coefficients near the like terms should be equal. Then, by comparing both sides, we can see that

`\begin{gathered} 5A+6B=1...(1) \\ and \\ A-5B=0...(2) \end{gathered}`

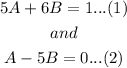
In matrix form, this system can be expressed as

`\begin{bmatrix}{5} & {6} \\ {-5} & {25}\end{bmatrix}\begin{bmatrix}{A} & {} \\ {B} & {}\end{bmatrix}=\begin{bmatrix}{1} & {} \\ {0} & {}\end{bmatrix}`

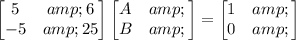
So, we need to solve this system of equations. This system is equivalent to

`\begin{gathered} 5A+6B=1 \\ -5A+25B=0 \end{gathered}`

By adding our last equations, we get

`31B=1`

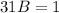
So B is given as

`B=(1)/(31)`

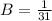
Now, by substituting this result into equation (2), we obtain

`A-5((1)/(31))=0`

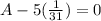
So A is given as

`A=(5)/(31)`

Therefore, the answer is:

`(x)/((6x-5)(5x+1))=((5)/(31))/(6x-5)+((1)/(31))/(5x+1)`