Question

Two cars drive on a straight highway. At time t = 0, car 1 passes mile marker 0 traveling due east with a speed of 20.0m/s. At the same time car 2 is 1.0km east of mile marker 0 traveling at 30.0m/s due west. Car 1 is speeding up with an acceleration of magnitude 2.5m/s2 and car 2 is slowing down with an acceleration of magnitude 3.2m/s2. (a) write x versus t equations of motion for both cars taking east as the positive direction. (b) At what time do the cars pass next to one another?

Answer 1

We know that

At time t = 0, car 1 passes mile marker 0 traveling due east with a speed of 20.0m/s. INITIAL SPEED OF CAR 1.

At the same time car 2 is 1 km east of mile marker 0 traveling at 30.0m/s due west. INITIAL SPEED OF CAR 2.

Car 1 acceleration is 2.5 m/s^2.

Car 2 acceleration is 3.2 m/s^2.

Let's create a diagram to visualize the problem.

Given that they are accelerated, we use the following formula.

`x=v_0t+(1)/(2)at^2`

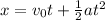
Let's use the magnitudes for each car to find their equations.

Car 1.

`x=20t+(1)/(2)\cdot2.5t^2\to x=20t+1.25t^2`

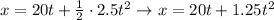
Car 2.

`x=1000-30t-(1)/(2)\cdot3.2t^2\to x=1000-30t-1.6t^2`

Note that the initial speed and acceleration are negative because car 2 is heading West. Also, observe that the initial position of car 2 is 1 km, that is, 1000 meters.

Now let's combine the equations to find t.

`\begin{gathered} 20t+1.25t^2=1000-30t-1.6t^2 \\ 1.25t^2+1.6t^2+20t+30t-1000=0 \\ 2.85t^2+50t-1000=0 \end{gathered}`

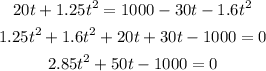
Using a calculator, we have the following solutions.

`\begin{gathered} t_1=11.9\sec \\ t_2=-29.5\sec \end{gathered}`

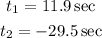
We take the positive solution because time can't be negative.

Therefore, they will pass next to one another after 11.9 seconds.