Question

(b) The equation of a straight line is given as follows: у | -1 3 2 PS The line cuts the x-axis at point P and the y-axis at point Q. (i) Find the coordinates of P and Q. (ii) Determine the gradient of the line.

Answer 1

We have the next given line equation:

`(x)/(3)-(y)/(2)=-1`

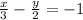
Now, solve for y to get the slope-intercept form y=mx+b.

`\begin{gathered} -(y)/(2)=-1+(x)/(3) \\ y=2(-1+(x)/(3)) \\ y=(2x)/(3)-2 \\ \end{gathered}`

Where -2 represents the point where the line cuts the y-axis.

Hence, Q=(0,-2)

To find the x-intercept, set y=0:

`\begin{gathered} y=(2x)/(3)-2 \\ 0=(2x)/(3)-2 \\ \text{Solve for x:} \\ 2=(2x)/(3) \\ 2\cdot3=2x \\ 6=2x \\ (6)/(2)=x \\ x=3 \end{gathered}`

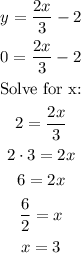
Hence, the P point is (3,0)

Now, the gradient is also called the slope.

The slope equation is given by:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \end{gathered}`

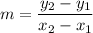
We can use the two points that we found before or we can get the slope looking at the slope-intercept form:

y=mx+b

where b represents the y-intercept and m represents the slope.

In this case, we found the next form:

`y=(2)/(3)x-2`

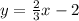
Hence, the gradient of the line is 2/3.