Question

Does the following infinite geometric series diverge or converge. explain.

Answer 1

- To begin, let us write the series in a general form:

`\begin{gathered} (1)/(5)+(1)/(10)+(1)/(20)+(1)/(40)+... \\ \\ \text{ Factorize }(1)/(5)\text{ out} \\ \\ (1)/(5)(1+(1)/(2)+(1)/(4)+(1)/(8)+...) \\ \\ (1)/(5)((1)/(2^0)+(1)/(2^1)+(1)/(2^2)+(1)/(2^3)+...) \\ \\ (1)/(5)+(1)/(5)((1)/(2)+(1)/(2^2)+(1)/(2^3)+...) \\ \\ (1)/(5)+(1)/(5)\sum_(k=1)^(\infty)(1)/(2^k) \end{gathered}`

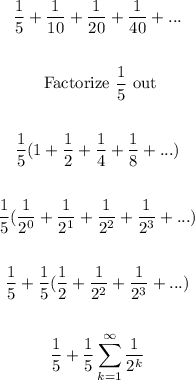
- From the above, we get a geometric series. Thus, we can apply the Ratio test

- The ratio test theorem states that:

`\begin{gathered} \text{ Let p be the limit below:} \\ p=\lim_(n\to\infty)|(a_(n+1))/(a_n)| \\ \\ \text{ If p exists and is less than 1, then the series converges} \\ \text{ if p exists and is greater than 1, then, the series diverges} \end{gathered}`

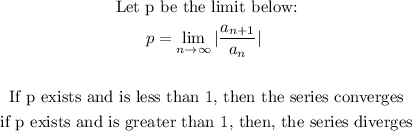
- Applying this theorem, we have:

`\begin{gathered} a_k=(1)/(2^k)=2^(-k) \\ a_(k+1)=(1)/(2^(k+1))=2^(-(k+1)) \\ \\ p=\lim_(k\to\infty)|(2^(-(k+1)))/(2^(-k))| \\ \\ p=\lim_(k\to\infty)|(2^(-k).2^(-1))/(2^(-k))| \\ \\ 2^(-k)\text{ crosses out} \\ \\ \therefore p=\lim_(k\to\infty)|2^(-1)| \\ \\ p=(1)/(2) \\ \\ \text{ This means that:} \\ p<1,\text{ implying that the series converges} \end{gathered}`

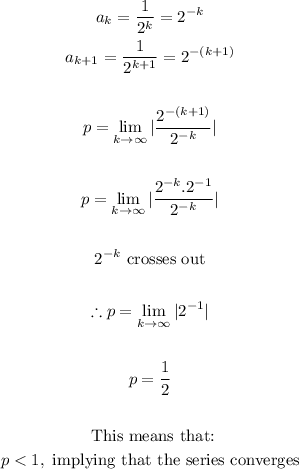
- Now that we know that the series converges, and it is a geometric series, we can apply the sum to infinity formula of a geometric series to find whether it has a sum or not.

- This is done below:

`\begin{gathered} (1)/(5)+(1)/(5)\sum_(k=1)^(\infty)(1)/(2^k) \\ \\ (1)/(5)+(1)/(5)((1)/(2)+(1)/(4)+(1)/(8)...) \\ \\ \text{ The geometric series portion of the sum has a common ratio of }(1)/(2)\text{ because:} \\ ((1)/(4))/((1)/(2))=((1)/(8))/((1)/(4))=(1)/(2) \\ \\ \text{ The formula for sum to infinity of a geometric sequence is:} \\ S_(\infty)=(a)/(1-r) \\ where, \\ a=First\text{ term} \\ r=common\text{ ratio} \\ \\ \therefore S_(\infty)=((1)/(2))/(1-(1)/(2))=1 \\ \\ \therefore(1)/(5)+(1)/(5)S_(\infty)=(1)/(5)+(1)/(5)(1)=(2)/(5) \\ \\ \text{ Thus, the series has a sum} \end{gathered}`

Final Answer

The series converges and the series has a sum