Question

State if the triangles are similar. If so, how do you know they are similar and complete the similarity statement.ΔABC ~ ____A. similar; AA similarity; ΔAVWB. similar; SSS similarity; ΔAVWC. similar; SAS similarity; ΔAVWD. not similar

Answer 1

We have the following triangles:

And we need to prove the similarity of both triangles by using any of the known theorems to determine that.

To find the similarity - if any - between the two triangles, we can proceed as follows:

1. We can observe that we only have the length of the sides for both triangles, then we can determine the length of the corresponding sides as follows:

• AC and AW are corresponding sides

,

• AB and AV are corresponding sides

,

• CB and WV are corresponding sides

2. Now, we can also observe that both triangles share the same angle A:

3. Then having this information, we can use the SAS similarity theorem to check if both triangles are similar, and this theorem says that it is sufficient, to prove that two triangles are similar, that two sets of corresponding sides are in proportion, and the angles (in this case, the angle A) they include are congruent. Then we have:

4. And the proportions are:

`\begin{gathered} (AC)/(AW)=(AB)/(AV) \\ \\ (24)/(16),(27+15)/(27)=(42)/(27) \\ \\ \text{ Then} \\ \\ (24)/(16)=(3)/(2)=1.5 \\ \\ (42)/(27)=(14)/(9)\approx1.555555... \\ \\ \therefore(42)/(27)\\e(24)/(16) \end{gathered}`

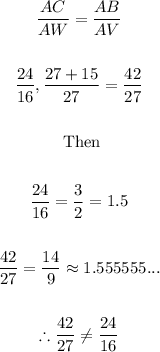
5. Since we obtained this result, that is, the corresponding are not in proportion, then both triangles are not similar.

Therefore, in summary, we can conclude that both triangles are not similar (option D.)