Question

Josef is turning two jump ropes for a game. The function L(t) represents the height, in cm, of the centerof the rope in his left hand t seconds after the game begins. Likewise, R(t) represents the height of thecenter of the rope in his right hand after t seconds.L(t) = 95 – 95 sin(t-2)R(t) = 95 + 95 sin(1462)Consider the following equation:95 - 95 sin95 +95 sin(72)What does the solution set for the last equation represent?

Answer 1

In the given problem, L(t) represents the height of the centre of the rope in the left hand, while R(t) represents the height of the centre of the rope in his right hand.

These functions are defined as,

`\begin{gathered} L(t)=95-95\sin ((\pi t)/(2)) \\ R(t)=95+95\sin ((\pi(t-2))/(2)) \end{gathered}`

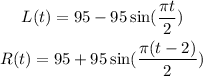
The equation is given as,

`95-95\sin ((\pi t)/(2))=95+95\sin ((\pi(t-2))/(2))`

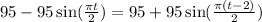
It follows that,

`L(t)=R(t)`

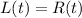
Clearly, the functions L(t) and R(t) are equated. That analytically means that we are equating the heights of the centres of the ropes in the left and right hand as well.

Resolve the equation as follows,

`\begin{gathered} 95-95\sin ((\pi t)/(2))=95+95\sin ((\pi(t-2))/(2)) \\ -95\sin ((\pi t)/(2))=95\sin ((\pi t)/(2)-\pi) \\ -\sin ((\pi t)/(2))=\sin \mleft\lbrace-(\pi-(\pi t)/(2))\mright\rbrace \\ -\sin ((\pi t)/(2))=-\sin (\pi-(\pi t)/(2)) \\ \sin ((\pi t)/(2))=\sin (\pi-(\pi t)/(2)) \end{gathered}`

Consider the formula,

`\sin x=\sin y\Rightarrow x=n\pi\pm y`

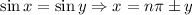
It follows that,

`(\pi t)/(2)=n\pi\pm(\pi-(\pi t)/(2))`

This is the implicit solution that gives the values of 't' in terms of 'n' which represents any whole number.

Thus, it can be concluded that the solution set of the equation represents the set of all numbers of seconds after the game begins when the centres of the left and right ropes have the same height.

Therefore, option D is the correct choice.