Step-by-step explanation:
From the table, the total sample space will be calculated below as
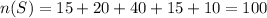
Concept:
To calculate the probability of throwing fewer than 3 pitches, we will use the formula
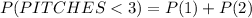
The probabaility of throwing 1 pitch is calculated below as
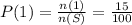
The probabaility of throwing 2 pitches is calculated below as
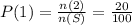
Hence, by susbtituting the values in the formula, we will have
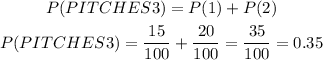
Hence,
The final answer is
