Question

What is the answer to this? i’m not sure how to complete the problem.

Answer 1

`a_(n)=a_(n-1)+(n-1)*4`

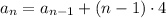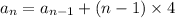
1) To get to know the answer to this problem, we need to consider the first term 15 the common difference obtained by the difference between the terms:

`\begin{gathered} 19-15=4 \\ 23-19=4 \\ 27-23=4 \end{gathered}`

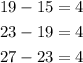
2) Therefore, we can write the recursive formula resorting to the previous term, i.e. our recursive formula is valid for the second term and so forth and so on.

`\begin{gathered} a_n=a_(n-1)+(n-1)d \\ \\ a_n=15+(2-1)4 \\ \\ a_2=15+4\Rightarrow a_2=19 \end{gathered}`

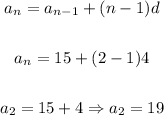
3) Thus, the answer is:

`a_n=a_(n-1)+(n-1)\cdot4`