Question

A quadrilateral has a perimeter of 32 and all side lengths are even integers. What is the probability that the quadrilateral is a square?

Answer 1

`a+b+c+d=32`

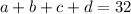
where a, b,c, and d are even integers.

The number of ways even integers can give 32 is

`12+12+4+4\text{ (rectangle)}`
`4+4+4+4\text{ (square)}`

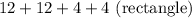
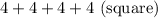
This is 2 combinations. We see that of the 2 combinations, there is only one (8+8

+8+8) that gives a square but this could also be a rhombus. Similarly, have 12+12+4+4 sides means we can have a rectangle as well as a parallelogram; thus we have 4 quadrilaterals that have even integer sides and only one combination gives a square; therefore, the probability of getting a square is 1/4.