Question

A hot air balloon is rising vertically with a velocity of 12.0 feet per second. A very small ball is released from the hot air balloon at the instant when it is 1280 feet above the ground. Use a(t)=−32 ft/sec2 as the acceleration due to gravity.1. How many seconds after its release will the ball strike the ground? Round the answer to the nearest two decimal places.2. At what velocity will it hit the ground?

Answer 1

1. 9.33 s

2. -286.47 ft/s

Step-by-step explanation:

We can calculate the number of seconds that it takes to strike the ground using the following equation

`y=y_i+v_it+(1)/(2)at^2`

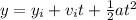
Where y is the height, yi is the initial height, vi is the initial velocity, a is the acceleration and t is the time.

The ball will hit the ground when y = 0 ft, so replacing yi = 1280 ft, vi = 12 ft/s, and a = -32 ft/s², we get:

`\begin{gathered} 0=1280+12t+(1)/(2)(-32)t^2 \\ 0=1280+12t-16t^2 \end{gathered}`

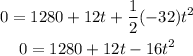
Solving for t, we get:

`\begin{gathered} -16t^2+12t+1280=0 \\ \text{ Using the quadratic equation, we get} \\ t=(-12\pm√(12^2-4(-16)(1280)))/(2(-16)) \\ \\ t=(-12\pm286.47)/(-32) \\ \\ Then \\ t=(-12+286.47)/(-32)=-8.57 \\ or\text{ t = }(-12-286.47)/(-32)=9.33 \end{gathered}`

Therefore, the ball will strike the ground at t = 9.33 m/s

Then, we can calculate the velocity using the following equation

`v_f=v_i+at`

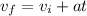
Replacing vi = 12 ft/s and a = -32 ft/s², we get:

`\begin{gathered} v_f=12+(-32)(9.33) \\ v_f=-286.47\text{ ft/s} \end{gathered}`

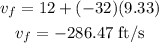
So, the final velocity is -286.47 ft/s

Therefore, the final answers are

1. 9.33 s

2. -286.47 ft/s