Question

The one-to-one functions g and h are defined as follows.g(x) = ***h={(-1, 4), (1, 2), (4, -1), (5, 6), (8, 7)}

Answer 1

Write out the functions given

`\begin{gathered} g(x)=(x+9)/(5) \\ h=((-1,4),(1,2),(4,-1),(5,6),(8,7)) \end{gathered}`

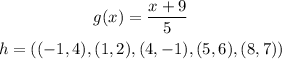
Find (a)

`(a)g^(-1)(x)`

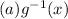
make x the subject of the function g(x) to get the inverse of g(x)

`\begin{gathered} g(x)=(x+9)/(5) \\ x+9=5* g(x) \\ x=5* g(x)-9 \end{gathered}`

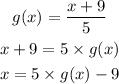
Substitute x for g(x) to get the inverse function of g(x). Therefore,

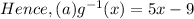
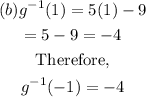
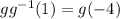
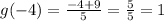
`Hence,(a)g^(-1)(x)=5x-9`
`\begin{gathered} (b)g^(-1)(1)=5(1)-9 \\ =5-9=-4 \\ \text{Therefore,} \\ g^(-1)(-1)=-4 \end{gathered}`

`gg^(-1)(1)=g(-4)`
`g(-4)=(-4+9)/(5)=(5)/(5)=1`

Hence,

`g\mathrm{}g^(-1)(1)=1`

Find (c)

From the h function given,

`h^(-1)(4)=-1`

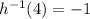
Hence,

(a) g-¹= 5x - 9

(b) g.g-¹= 1

(c)h-¹ = -1