SOLUTION
Given the information in the question, the following steps help to solve the question
Step 1: Write out the mathematical interpretations of the statements:
After 2 hours, Rachel is 13 miles from the campground.
After 4 hours, Rachel is 6 miles from the campground.
Step 2: Write the interpretations in form of points, we have:
x as the number of hours and y as the number of miles from the campground.
Therefore, we have two points (2,13) and (4,6).

Step 3: We find the slope of the graph using the point gotten:
The equation of the line passing through the points is:
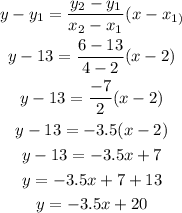
Step 4: Get the slope using the general equation of a line
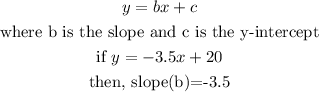
Hence, the slope of the graph is -3.5 and this means that the rate at which Rachel's distance from the campground changes per hour is 3.5 miles which is option B.