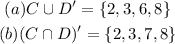Question

Sets C and D are subsets of the universal set U.These sets are defined as follows.U=(2, 3, 6, 7, 8)C={6,8}D={6,7}Find the following sets.Write your answer in roster form or as Ø.(a) C U D' =(b) (C n D)' =

Answer 1

Given:

The universal set is,

`U=\lbrace2,3,6,7,8\rbrace`

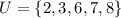
The set C is,

`C=\lbrace6,8\rbrace`

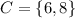
The set D is,

`D=\lbrace6,7\rbrace`

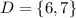
Required:

To find the sets in roster form.

`\begin{gathered} (a)C\cup D^(\prime) \\ (b)(C\cap D)^(\prime) \end{gathered}`

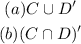
Step-by-step explanation:

The sets given are,

`\begin{gathered} U=\lbrace2,3,6,7,8\rbrace \\ C=\lbrace6,8\rbrace \\ D=\lbrace6,7\rbrace \end{gathered}`

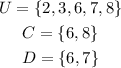
Then

(a) The set D' is,

`D^(\prime)=\lbrace2,3,8\rbrace`

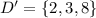
Thus, the required set is given by,

`\begin{gathered} C\cup D^(\prime)=\lbrace6,8\rbrace\cup\lbrace2,3,8\rbrace \\ \Rightarrow C\cup D^(\prime)=\lbrace2,3,6,8\rbrace \end{gathered}`

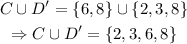
(b) The intersection of C and D is given by,

`C\cap D=\lbrace6\rbrace`

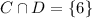
Thus, the compliment of the above set is the required set given by,

`(C\cap D)^(\prime)=\lbrace2,3,7,8\rbrace`

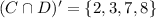
Final Answer:

The required sets in roster form are,

`\begin{gathered} (a)C\cup D^(\prime)=\lbrace2,3,6,8\rbrace \\ (b)(C\cap D)^(\prime)=\lbrace2,3,7,8\rbrace \end{gathered}`