Question

How do I solve this, I don’t understandhow to solve

Answer 1

The rectangular garden has an area of 33 ft².

The length of the garden (l) is 4ft less than 7 times the width. If "w" represents the width, then the length of the garden can be expressed as follows:

`l=7w-4`

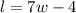
The area of the garden is equal to the product between the length and the width:

`\begin{gathered} A=lw \\ \end{gathered}`

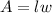
Substitute A=33 and l=7w-4 in the formula:

`\begin{gathered} A=lw \\ 33=w(7w-4) \end{gathered}`

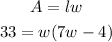
Distribute the multiplication on the parentheses term:

`\begin{gathered} 33=w\cdot7w-w\cdot4 \\ 33=7w^2-4w \end{gathered}`

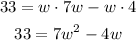
Zero the equation by subtracting 33 to both sides of the equal sign:

`\begin{gathered} 33-33=7w^2-4w-33 \\ 7w^2-4w-33=0 \end{gathered}`

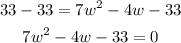
Now that we have determined a quadratic expression for the area of the rectangular garden, we can determine the possible values of the width using the quadratic equation.

In this case, the independent variable is "w" which corresponds to the variable "x" in the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\to \\ w=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

Where

a is the coefficient of the quadratic term, in this case, a= 7.

b is the coefficient of the "x-term", in this case, b= -4.

c is the constant of the quadratic expression, in this case, c= -33.

Replace the values in the formula and solve:

`\begin{gathered} w=\frac{-(-4)\pm\sqrt[]{(-4)^2-4\cdot(-33)\cdot7}}{2\cdot7} \\ w=\frac{4\pm\sqrt[]{16+84}}{14} \\ w=\frac{4\pm\sqrt[]{100}}{14} \\ w=(4\pm10)/(14) \end{gathered}`

-Addition

`\begin{gathered} w=(4+10)/(14) \\ w=(14)/(14) \\ w=1ft \end{gathered}`

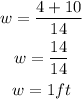
-Subtraction

`\begin{gathered} w=(4-10)/(14) \\ w=-(6)/(14) \\ w=-(3)/(7)ft \end{gathered}`

Both values are correct, but lengths cannot be negative, then the width cannot be equal to -3/7ft.

The width of the rectangular garden is w=1 ft

Calculate the length:

`\begin{gathered} l=7w-4 \\ l=7\cdot1-4 \\ l=3ft \end{gathered}`

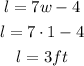
The length of the rectangular garden is l=3ft