Question

How do you graph polynomial functions? Just a sketch. For example, f(x)= (x-5)(x+1)(x^2-3x+2).

Answer 1

Step-by-step explanation

The key features we have to identify to sketch the graph of a polynomial function are:

• The zeros (or roots) of the polynomial

,

• The local maximums/minimums

,

• The end behavior

This polynomial is almost completely factored. Let's factor the last factor to find the other two zeros,

`x^2-3x+2=0`

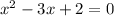
Using the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case, a = 1, b = -3, and c = 2,

`\begin{gathered} x=\frac{3\pm\sqrt[]{3^2-4\cdot1\cdot2}}{2\cdot1}=\frac{3\pm\sqrt[]{9-8}}{2}=(3\pm1)/(2) \\ x=1;x=2 \end{gathered}`

So the full factored form of the polynomial is,

`f(x)=(x-5)(x+1)(x-1)(x-2)`

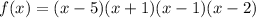
As we can see, the zeros of the polynomial are -1, 1, 2, and 5.

The end behavior is determined by the degree of the polynomial and the sign of the leading coefficient,

Since the coefficient of x in every factor is 1, the leading coefficient must be 1. Also, we have 4 factors with no multiplicity, so the degree of the polynomial is 4. Therefore, the end behavior is f(x) → ∞ when x approaches ∞ or -∞.

Now, we have to find the local maximums or minimums. Between two zeros, there is always a local maximum or minimum.

Before the first zero, x = -1, the function comes from infinity, crosses the x-axis at x = -1, and there msut be a minimum between x = -1 and x = 1 because the function must go up again and cross the x-axis again.

Following the same reasoning, between x = 1 and x = 2 there is a maximum and between x = 2 and x = 5 there is a minimum.

Hence, the graph should be something like this,