Question

Can you please help me with 27Please give all forms of the end behavior such as ups/downs, as_,_, and limits

Answer 1

Answer:

`\lim _(x\to-\infty)f(x)=\lim _(x\to\infty)f(x)=-2`

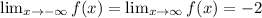
Explanation:

Given a rational function, the end behavior of its graph is how the graph behaves as x approaches infinity or negative infinity.

In the function f(x) below:

`f(x)=-(2x)/(x-6)`

• The degree of the numerator = 1

,

• The degree of the denominator = 1

Since the degrees of the numerator and the denominator are the same, divide the coefficients of the leading terms to obtain the horizontal asymptote.

`\text{Horizontal Asymptote, }y=-(2)/(1)=-2`

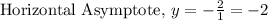
Thus, for f(x):

`\begin{gathered} \lim _(x\to-\infty)f(x)=-2 \\ \lim _(x\to\infty)f(x)=-2 \end{gathered}`

The function approaches -2 as x tends to positive and negative infinity.

Next, we determine the vertical asymptote of f(x) by setting the denominator equal to 0 and solving for x.

`\begin{gathered} x-6=0 \\ x=6 \end{gathered}`

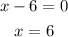
What this means is that in f(x), the value of f(x) is undefined at x=6.