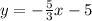The form of the equation of the line is
y = m x + b, where
m is the slope
b is the y-intercept
The rule of the slope is

(x1, y1) and (x2, y2) are two points on the line
To find the equation of the perpendicular bisector to the line whose endpoints are (-8, -3) and (2, 3), we must find the slope of this line
x1 = -8 and y1 = -3
x2 = 2 and y2 = 3
Substitute them in the rule above

To find the slope of the perpendicular line reciprocal the fraction and change its sign
The slope of the perpendicular line is

Substitute it in the form of the equation
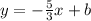
To find b we must have a point on the line
Since the line is the bisector of the given line, then it passes through its mid-point, then we need to find the mid-point of the given line
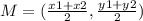
We will use the endpoints above
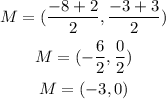
The mid-point is (-3, 0)
We will use it to find b
Substitute x by -3 and y by 0 in the equation to find b
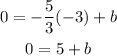
Subtract 5 from both sides
-5 = b + 5 - 5
-5 = b
Substitute it in the equation
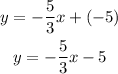
The equation of the perpendicular bisector is