ANSWER
19.68 feet
Step-by-step explanation
The tennis ball dropped on a surface that is 10 feet high and each time it dropped, it was 1/2 as high as the preceeding one.
This represents a geometric series with first term 10 and common ratio of 1/2.
The general form of a geometric series is:
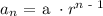
where an = nth term
r = common ratio
We have to find the total height it would have traveled when it hits the surface the 6th time.
This means that we have to find the sum of the heights it reached for those 6 times.
We use the formula for the sum of a geometric sequence:
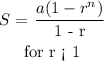
Therefore, we have:

Therefore, the ball would have reached a total height of 19.68 feet by the time it bounced the 6th time.