Question

The base model of a 2016 Jeep Wrangler Sport with a tow package cost $24,290. When equipped with a tow package and a hard top, the vehicle's price rose to $25,285. The cost of the base model with a hard top was $24,890. Find the base price, the cost of a tow package, and the cost of a hard top.

Answer 1

Let the base price be x, cost of tow package be y and cost of hard be z.

So equation for three variables are,

`x+y=24290`
`x+y+z=25285`
`x+z=24890`

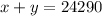
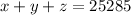
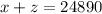
Substract equation x + z = 24890 from equation x + y + z = 25285 to obtain the value of y.

`\begin{gathered} x+y+z-(x+z)=25285-24890 \\ y=395 \end{gathered}`

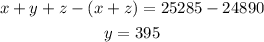
Substract equation x + y = 24290 from x + y + z = 25285 to obtain the value of z.

`\begin{gathered} x+y+z-(x+y)=25285-24290 \\ z=995 \end{gathered}`

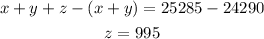
Substitute the values in the equation x + y +z = 25285 to obtain the value of x.

`\begin{gathered} x+395+995=25285 \\ x=25285-1390 \\ =23895 \end{gathered}`

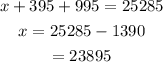
So base price is $23895, cost of tow package is $395 and cost of hard top is $995.