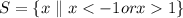
Step-by-step explanation
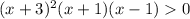
Step 1
solve for each factor:
set each factor equal to zero
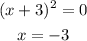
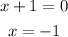
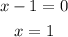
so, we have 3 critical numbers
-3,-1 and 1
Step 2
now, let's make a table to evaluate each interval , (select a number from the interval)
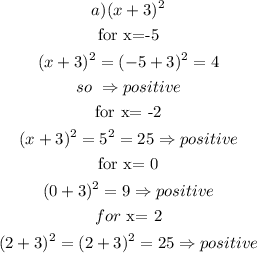
b) (x+1)
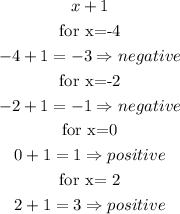
c)(x-1)
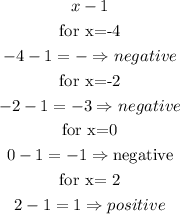
Step 3
now, make th multiplication of the signs ( check the table in step 2)
so, we got
(-infi, -1) U (1, inf)
as we need that the product of the factors is greater than zero ( positive) , the solution is( set notation)
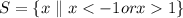
I hope this helps you