The given line in the question is
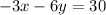
Two lines are said to be parallel when their gradients or slope are equal
That is
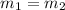
The general equation of a line is given as
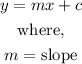
Step 1: Make y the subject of the formula from the equation -3x-6y=30
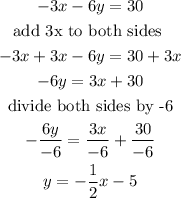
From the equation above by comparing coefficient, the slope is
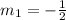
Step 2: Check which of the equations will have the same slope of -1/2
The first equation given in the question is

The second equation given is
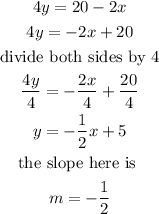
The third equation given is
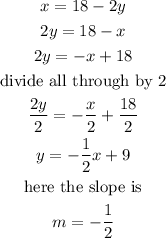
The fourth equation given is

The fifth equation given is

The sixth equation given is
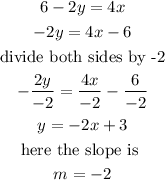
Hence,
The equations parallel to -3x-6y=30 are
4y=20-2x
x=18-2y
5x+10y=10