Question

which equation are parallel to the line -3x-6y=30? CAN YOU PLEASE CHECK THAT EQUATIONS WHICH IS CORRECT???

Answer 1

The given line in the question is

`-3x-6y=30`

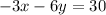
Two lines are said to be parallel when their gradients or slope are equal

That is

`m_1=m_2`

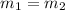
The general equation of a line is given as

`\begin{gathered} y=mx+c \\ \text{where,} \\ m=\text{slope} \end{gathered}`

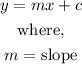
Step 1: Make y the subject of the formula from the equation -3x-6y=30

`\begin{gathered} -3x-6y=30 \\ \text{add 3x to both sides } \\ -3x+3x-6y=30+3x \\ -6y=3x+30 \\ \text{divide both sides by -6} \\ -(6y)/(-6)=(3x)/(-6)+(30)/(-6) \\ y=-(1)/(2)x-5 \end{gathered}`

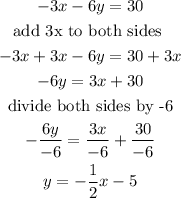
From the equation above by comparing coefficient, the slope is

`m_1=-(1)/(2)`

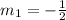
Step 2: Check which of the equations will have the same slope of -1/2

The first equation given in the question is

`\begin{gathered} 2x-y=15 \\ \text{substract 2x from both sides} \\ 2x-2x-y=15-2x \\ -y=-2x+15 \\ \text{divide both sides by -1} \\ -(y)/(-1)=-(2x)/(-1)+(15)/(-1) \\ y=2x-15 \\ \text{the slope here is m =2} \end{gathered}`

The second equation given is

`\begin{gathered} 4y=20-2x \\ 4y=-2x+20 \\ \text{divide both sides by 4} \\ (4y)/(4)=-(2x)/(4)+(20)/(4) \\ y=-(1)/(2)x+5 \\ \text{the slope here is } \\ m=-(1)/(2) \end{gathered}`

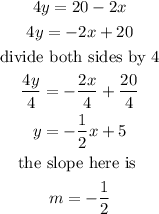
The third equation given is

`\begin{gathered} x=18-2y \\ 2y=18-x \\ 2y=-x+18 \\ \text{divide all through by 2} \\ (2y)/(2)=-(x)/(2)+(18)/(2) \\ y=-(1)/(2)x+9 \\ \text{here the slope is} \\ m=-(1)/(2) \end{gathered}`

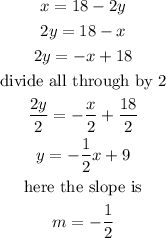
The fourth equation given is

`\begin{gathered} y=-3x+1 \\ \text{here the slope is} \\ m=-3 \end{gathered}`

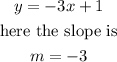
The fifth equation given is

`\begin{gathered} 5x+10y=10 \\ \text{substract 5s from both sides} \\ 5x-5x+10y=10-5x \\ 10y=-5x+10 \\ \text{divide both sides by 10} \\ (10y)/(10)=-(5x)/(10)+(10)/(10) \\ y=-(1)/(2)x+1 \\ \text{here the slope is} \\ m=-(1)/(2) \end{gathered}`

The sixth equation given is

`\begin{gathered} 6-2y=4x \\ -2y=4x-6 \\ \text{divide both sides by -2} \\ -(2y)/(-2)=(4x)/(-2)-(6)/(-2) \\ y=-2x+3 \\ \text{here the slope is } \\ m=-2 \end{gathered}`

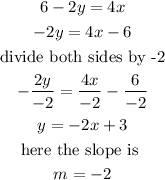
Hence,

The equations parallel to -3x-6y=30 are

4y=20-2x

x=18-2y

5x+10y=10