Question

Write a quadratic function in standard form whose graph passes through (-8,0), (1,0), and (2, 30).

Answer 1

y = 3x² + 21x - 24

Step-by-step explanation:

A quadratic function can be expressed in the following form:

y = a(x-p)(x-q)

Where p and q are the x-intercepts of the graph. Since the graph passes through the points (-8, 0) and (1, 0), we can say that the x-intercepts are -8 and 1. So, the equation can be written as:

y = a(x - (-8))(x - 1)

y = a( x + 8)( x - 1)

Now, we need to find the value of a, so using the point (2, 30), we can write the following equation:

y = a( x + 8)( x - 1)

30 = a(2 + 8)( 2 - 1)

So, solving for a, we get:

`\begin{gathered} 30=a(10)(1) \\ 30=a\cdot(10) \\ (30)/(10)=(a\cdot10)/(10) \\ 3=a \end{gathered}`

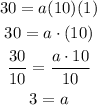
Therefore, the equation of the quadratic function that passes through the points (-8,0), (1,0), and (2, 30) is:

`y=3(x+8)(x-1)`

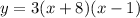
Finally, to write the equation in standard form, we need to solve the expression as follows:

`\begin{gathered} y=(3x+3\cdot8)(x-1) \\ y=(3x+24)(x-1) \\ y=(3x\cdot x)-(3x\cdot1)+(24\cdot x)-(24\cdot1) \\ y=3x^2-3x+24x-24 \\ y=3x^2+21x-24 \end{gathered}`

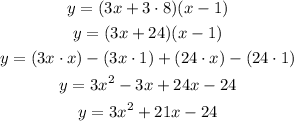
So, the answer is:

y = 3x² + 21x - 24