Question

Roy is a veterinarian at the small-animal clinic. He has 4 appointmentsscheduled for Monday Morning two new-patient appointments, a serious injury visitand a dental sealing in hours, how muchtime should these appointments take.Sick Animal visit 1/2 hrNew patient Appts : 3/4 hrSerious injury visit 1 1/4 hrdental scaling 3/4 hrImmunizations 1/4 hrRoutine physical 1/3 hr

Answer 1

So we have to find how much time those 4 appointments will take. Since the duration of each appointment is given in fractions it's important to remember a properties of fractions:

`\begin{gathered} (b)/(a)+(c)/(a)=(b+c)/(a) \\ 1=(a)/(a) \end{gathered}`

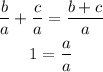
It is also important to remember the relation between the mix number notation and the usual fraction number notation:

`a\text{ }(b)/(c)=a+(b)/(c)`

With all of this in mind we can start working on the question. The four appointments consist of two 3/4 hr new patient visits, one 1 1/4 hr serious injury visit and one 3/4 hr dental sealing. The time it will take Roy to finish all of them (t) is equal to the sum of their individual times:

`t=(3)/(4)+(3)/(4)+1\text{ }(1)/(4)+(3)/(4)`

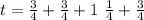
Using what we saw about mix number notation and fractions we get:

`\begin{gathered} 1\text{ }(1)/(4)=1+(1)/(4) \\ 1+(1)/(4)=(4)/(4)+(1)/(4)=(4+1)/(4)=(5)/(4) \\ 1\text{ }(1)/(4)=(5)/(4) \end{gathered}`

Then we have:

`t=(3)/(4)+(3)/(4)+(5)/(4)+(3)/(4)=(3+3+5+3)/(4)=(14)/(4)=(7)/(2)`

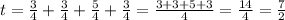
So the answer is 7/2 hours.