Question

In right triangle ABC shown below,what is the length of AC?

Answer 1

In any right triangle, we can apply the Pythagorean Theorem, which says that:

`a^2+b^2=c^2`

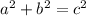
Where a and b are the legs of the right triangle and c is the hypotenuse of the triangle.

The hypotenuse is the greter side, the one oposite to the right angle. In this case, it is AC.

The other sides are the legs and, for the Pythagorean Theorem, we can set either one as a and b.

So, we can right:

`\begin{gathered} AB^2+BC^2=AC^2 \\ 6^2+8^2=AC^2 \\ AC^2=36+64 \\ AC^2=100 \\ AC=√(100) \\ AC=10 \end{gathered}`

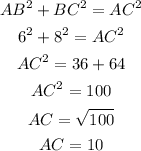
So, the length of AC is 10.