we have the function
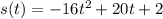
this function represents a vertical parabola open downward
the vertex represents a maximum
Convert the given function to vertex form
so
y=a(x-h)^2+k
where
(h,k) is the vertex
step 1
Factor of -16
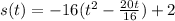
step 2
Complete the square
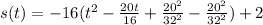
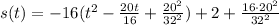
simplify
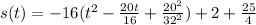
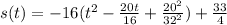
Rewrite as perfect squares
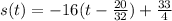
simplify
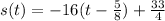
the vertex is the point (5/8,33/4)
therefore
the maximum height is the y-coordinate of the vertex
maximum height is 33/4=8.25 ft