Question

Write an equation for the parabola whose vertex is at (2,7) and which passes through (4,2)

Answer 1

We can write the equation of a parabola in to forms.

The standard form:

`y=ax^2+bx+c`

Or the vertex form:

`y=a(x-h)^2+k`

Where the point (h,k) is the vertex. We are going to use this one to solve this problem.

We have that the vertex coordinates are (2,7), so h=2 and k=7. So we have the formula:

`y=a(x-2)^2+7`

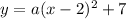
We just need to find a. For this we use the second point given (4,2). Replace x=4 and y=2 in the formula ans solve for a:

`2=a(4-2)^2+7`
`2-7=a(2)^2`
`-5=4a`
`a=-(5)/(4)`

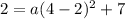
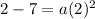
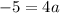
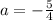
Then we have the complete equation for the given parabola:

`y=-(5)/(4)(x-2)^2+7`

To write it in the standard form we just have to use the binomial squared fomula:

`y=-(5)/(4)(x^2-4x+4)^{}+7`
`y=-(5)/(4)x^2+5x-5^{}+7`
`y=-(5)/(4)x^2+5x+2`

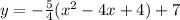
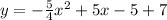
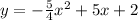
And in the standard form a = -5/4, b=5 and c=2