The given expression is:
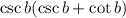
It is required to simplify the expression to a single trigonometry function.
To do this, trigonometric identities have to be applied to simplify the expression.
The following trigonometry identities will be used:
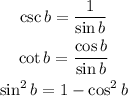
Use the inverse trigonometry identities to rewrite the expression as:
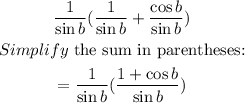
Multiply the expressions:
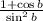
Rewrite the denominator using the trigonometric identity:
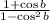
Rewrite the denominator further using the difference of two squares of binomials:
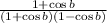
Cancel out like terms in the numerator and denominator, so the expression becomes:
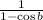
Hence, the required answer.