Given that you have to verify that:
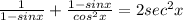
You need to follow these steps, in order to solve the exercise:
1. You need to use this Pythagorean Identify to rewrite the denominator of the second fraction:
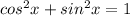
If you solve for:
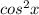
You get:
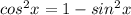
Then, you can rewrite the expression on the right side in this form:
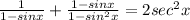
2. By definition:
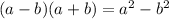
Then, you can rewrite the denominator of the second fraction in this form:
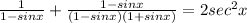
3. Now you can cancel common terms:
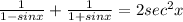
4. Add the fractions using this formula for adding fractions with different denominators:
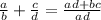
Then, you get:
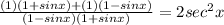
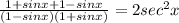
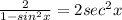
5. You already know that:
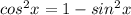
Then, you can rewrite the denominator as:
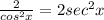
6. Remember this Reciprocal Identify:
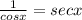
Therefore, you can determine:
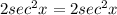
Hence, the answer is: