The inequality is given to be:
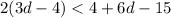
Step 1: Simplify the right-hand side of the inequality
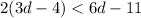
Step 2: Expand the bracket on the left-hand side of the inequality
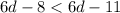
Step 3: Add 8 to both sides of the inequality
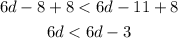
Step 4: Subtract 6d from both sides of the inequality
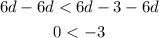
Since we know that 0 is actually greater than -3, it means that the statement above is untrue.
Therefore, the inequality has NO SOLUTION.