- The domain of a function f(x) is the set of all values for which the function is defined.
- The range of the function is the set of all values that f takes.
In our problem we have the following function:
![f(x)=\sqrt[]{9-x^2}](https://img.qammunity.org/2023/formulas/mathematics/college/eut110jtzdblmimfe5txdix9k10vaff6cr.png)
Domain
In order to find the domain we must look for the values of x for which the function is defined.
We see that the function has a square root, if we want to have a function with real values, the argument of the square root must be positive. So we need to find the values of x such that:
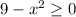
From the last equation we see that:
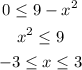
So the values of x must me in the interval: [-3,3] (domain)
Why? Because if replace, for example x = 4, in the equation of our function, we see that we get the square root of a negative number!
Range
In order to find the range of the function, we must look for the values of f(x) in the domain of the function.
- First, we can see that we only can have positive values for our function. So in principle the domain is: [0,∞)
- Second, we must see if our function has a maximum value. We see that the maximum value of our function is get it when we replace x = 0, and we get: f(0) = √9 = 3
Taking in account the last results, we see that the range of our function is: [0,3]
Summary
- Domain: [-3,3]
- Range: [0,3]