A vertical parabola with vertex (1,-4) and focus (1,-2) is given. It is required to find the standard form of the equation for the parabola.
Recall that the equation of a Vertical Parabola with vertex (h,k) and focus (h,k+1/4a) is given as:
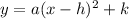
Compare the given vertex (1,-4) with the form (h,k). It follows that:
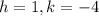
Compare the given focus (1,-2) with the form (h,k+1/4a). It follows that:
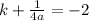
Substitute k=-4 into the equation and find the value of a:
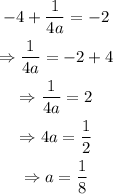
Substitute k=-4, h=1, and a=1/8 into the equation of a vertical parabola:
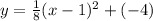
Rewrite the equation in standard form as follows:
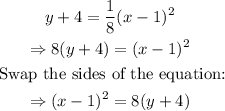
Recall that the Directrix of a vertical parabola is represented by the equation:
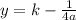
Substitute k=-4 and a=1/8 into the equation of directrix:
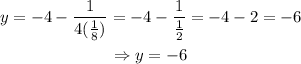
Hence, the correct answer is (x-1)²=8(y+4); y=-6.
The correct answer is (x-1)² = 8(y+4) ; y = - 6. (second option)