Question

The graph of a function is shown on the coordinate plane below. Which relationship represents a function with a greater slope than the function graphed?

Answer 1

Identify the slope of each of the given functions in order to compare them with the slope of the function whose graph is given.

From the graph, notice that the line goes down 3 squares for each square it goes to the right. Then, the slope of the function whose graph is given is -3.

Use the slope formula to find the slope of the relationships shown in options A and B:

`m=(y_2-y_1)/(x_2-x_1)`

A)

Notice that (3,1) and (5,5) are two pairs of values for x and y from the table.

Replace these values into the slope formula to find the slope of the relationship:

`m=(5-1)/(5-3)=(4)/(2)=2`

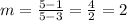
B)

The pairs (5,-29) and (7,-39) belong to this relationship. Replace these values into the slope formula:

`m=((-39)-(-29))/(7-5)=(-39+29)/(2)=(-10)/(2)=-5`

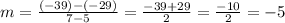
Use the slope-intercept form of the equation of a line to find the slope of the relationships shown in options C and D:

`y=mx+b`

Notice that when the variable y is isolated, the slope of the line is the coefficient of the variable x.

C)

The coefficient of x is -3. Then, the slope of this line is -3.

D)

The coefficient of x is -4. Then, the slope of this line is -4.

The slopes of the relationships from the options A, B, C and D are 2,-5,-3 and -4, respectively.

The only number from 2,-5,-3 and -4 which is greater than -3 is 2, the slope of the relationship shown in option A.

Therefore, the relationship that represents a function with a greater slope than the unction graphed is that of option A.

The correct choice is: option A.