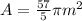Question

The radius of a circle is 6 meters. What is the area of a sector bounded by a 114° arc?Give the exact answer in simplest form. ____ square meters. (pi, fraction,)

Answer 1

We need to find the area of a sector of circle, bounded by a 114° arc. That sector is a fraction of the circumference, let's calculate it:

We have an arc of 114°, while the complete circumference has 360°.

The fraction of circle from we are going to calculate the area is:

`(114)/(360)`

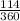
Now, we can estimate the total area of the circle of radius 6, and then multiply it by the fraction of circumference that concerns us: 114/360.

The area of the cicle is:

`\pi\cdot r^2=\pi\cdot(6m)^2=36\pi m^2`

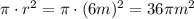
Now, the area of the sector is:

`A=(114)/(360)\cdot36\pi m^2`

360 is ten times 36, so:

`A=(114)/(10)\pi m^2`

Now simplifying, the half of 114 is 57, while the half of 10 is 5, then:

`A=(57)/(5)\pi m^2`