Question

Find the equation of the given line.Find the equation of the line passing through (1, 2) and (4,8).y =

Answer 1

In order to find the equation of the line, you take into account that the general form of the equation of a line is:

`y=mx+b`

where m is the slope and b is the y-intercept.

You calculate the slope m of the line by using the following formula:

`m=\frac{y_2-y_1}{x_2-x_1_{}}`

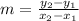
where (x1,y1) and (x2,y2) are two points of the line. You use the given points (1,2) and (4,8):

`m=(8-2)/(4-1)=(6)/(3)=2`

Next, you use again the formula for the slope, but in the following way:

`m=(y-y_1)/(x-x_1)`

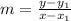
where (x1,y1) is a point of the line. You use the point (1,2):

`m=(y-2)/(x-1)`

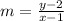
Next, you solve the previous equation for y, then you replace the value of m and put the equation in the slope y-intercept form:

`\begin{gathered} m=(y-2)/(x-1) \\ m(x-1)=y-2 \\ mx-m=y-2 \\ mx-m+2=y \\ 2x-2+2=y \\ y=2x \end{gathered}`

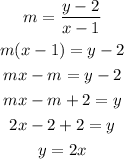
Hence, the equation of the line is y = 2x