Question

Answer the questions below about the quadratic function.g(x) = -x + 6x-8Does the function have a minimum or maximum value?MinimumMaximumWhere does the minimum or maximum value occur?X =.What is the function's minimum or maximum value?

Answer 1

#A

The function given to us is a quadratic equation of the form:

`g(x)=-x^2+6x-8`

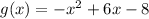
We are asked to figure out whether or not the function has a minimum or maximum value.

Generally, the equation of the form:

`y=ax^2+bx+c`

has a graph that looks like this:

While functions of the form:

`y=-ax^2+bx+c`

have graphs that look like this:

Since the function given to us is similar to this second function because of the negative coefficient of x-squared, we know that the function given has a maximum value.

Hence, the answer to the first question is:

"The graph has a Maximum value"

#B

The next part of the question asks us where this maximum value occurs.

In order to solve this, we must follow a couple of steps:

1. We differentiate the function to find the equation of the slope of the function.

2. We equate the slope function to zero because at the maximum value, the graph stops changing i.e. the slope becomes zero.

3. We find x from the slope function equated to zero in step 2. This is the value of x for which the original equation has its maximum value.

4. Substitute the value of x into the original equation to find the value of y. This value of y would be the maximum value.

Now, let us use the following steps to solve.

1. We differentiate the function to find the equation of the slope of the function.:

`\begin{gathered} g(x)=-x^2+6x-8 \\ \text{differentiating the function} \\ g^(\prime)(x)=-2x+6 \end{gathered}`

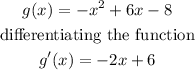
The above function g'(x) is the slope function of the quadratic equation.

2. We equate the slope function to zero because at the maximum value, the graph stops changing i.e. the slope becomes zero.

`\begin{gathered} g^(\prime)(x)=-2x+6 \\ \text{equate g'(x) to zero to find maximum value} \\ -2x+6=0 \end{gathered}`

3. We find x from the slope function equated to zero in step 2. This is the value of x for which the original equation has its maximum value.

`\begin{gathered} -2x+6=0 \\ \text{subtract 6 from both sides} \\ -2x=-6 \\ \text{divide both sides by -2} \\ -(2x)/(-2)=-(6)/(-2) \\ \\ \therefore x=3 \end{gathered}`

Now, to find the maximum value, at x = 3

4. Substitute the value of x into the original equation to find the value of y. This value of y would be the maximum value.

`\begin{gathered} y=-x^2+6x-8 \\ \text{put x = 3} \\ y=-3^2+6(3)-8 \\ y=-9+18-8 \\ \\ \therefore y=1\text{ (Maximum value)} \end{gathered}`

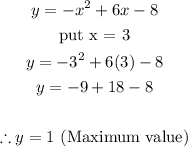
Therefore, the maximum value is: y = 1