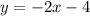Question

Write the slope-intercept form of the equation.Passes through (-1,-2) and parallel to y=-2x-1

Answer 1

The slope-intercept form of the equation is;

`y=-2x-4`

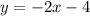
Step-by-step explanation:

Given that the equation passes through;

`(-1,-2)`

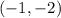
And is parallel to the equation;

`y=-2x-1`

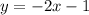
We can derive the slope from the equation parallel to it;

`m=-2`

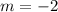
Using the point-slope formula;

`y=m(x-x_1)+y_1`

Substituting the point and the slope;

`\begin{gathered} y=-2(x+1)-2 \\ y=-2x-2-2 \\ y=-2x-4 \end{gathered}`

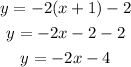
Therefore, the slope-intercept form of the equation is;

`y=-2x-4`