Question

Does this table represent a linear function or a non-linear function?

Answer 1

Concept:

To figure out if the value on the table is a linear or non-linear function, we will calculate their slopes individually to give the same value

To determine whether the function is linear or nonlinear, see whether it has a constant rate of change. Pick the points in any two rows of the table and calculate the rate of change between them. The first two rows are a good place to start. Now pick any other two rows and calculate the rate of change between them.

The coordinates of the table are given below as

`\begin{gathered} (-1,2)\Rightarrow x_1=-1,y_1=2 \\ (0,4)\Rightarrow x_2=0,y_2=4 \\ (1,6)\Rightarrow x_3=1,y_3=6 \\ (2,8)\Rightarrow x_4=2,y_4=8 \end{gathered}`

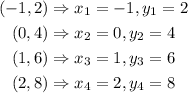
Step 1:

Calculate the slope using the formula below

`\text{slope}=m=(y_2-y_1)/(x_2-x_1)`

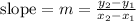
By substituting the values, we will have

`\begin{gathered} \text{slope}=m=(y_2-y_1)/(x_2-x_1) \\ m=(4-2)/(0-(-1)) \\ m=(2)/(1) \\ m=2 \end{gathered}`

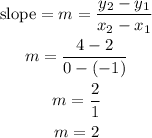
Step 2:

Calculate the slope using the formula below

`m=(y_3-y_2)/(x_3-x_2)`

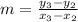
By substituting the values, we will have

`\begin{gathered} m=(y_3-y_2)/(x_3-x_2) \\ m=(6-4)/(1-0) \\ m=(2)/(1) \\ m=2 \end{gathered}`

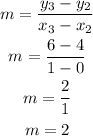
Step 3:

Calculate the slope using the formula below

`m=(y_4-y_3)/(x_3-x_2)`

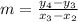
By substituting the values, we will have

`\begin{gathered} m=(y_4-y_3)/(x_3-x_2) \\ m=(8-6)/(2-1) \\ m=(2)/(1) \\ m=2 \end{gathered}`

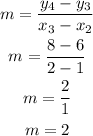
From the calculations above, we can see that the slopes remain constant using different pairs of coordinates on the table of values.

Using a graphing calculator, we will have the graph of the table to be

To determine the function of the line on the table of values, we will use the formula below

`m=(y-y_1)/(x-x_1)`

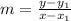
By substituting the values, we will have

`\begin{gathered} m=(y-y_1)/(x-x_1) \\ (2)/(1)=(y-2)/(x-(-1)) \\ (2)/(1)=(y-2)/(x+1) \\ 1(y-2)=2(x+1) \\ y-2=2x+2 \\ y=2x+2+2 \\ y=2x+4 \end{gathered}`

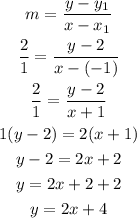
Hence,

The table represents a LINEAR function

The first OPTION is the right answer